Edição 53, junho de 2010
Por Délvio F. Bernardes, Fernando N. Belchior, Francisco J. D. M. Galvão Júnior, Ivan P. Faria, José P. G. Abreu, Jocélio S. Sá, Marcel F. C. Parentoni e Paulo M. Silveira.
Resultados revelam que, para a situação comparativa abordada no artigo, as perdas elétricas aumentam cerca de 8% quando os transformadores alimentam cargas não lineares
Cargas não lineares causam a circulação de correntes não senoidais em equipamentos elétricos (transformadores, cabos, reatores, etc.) instalados entre a fonte de alimentação e a carga.
O incremento das perdas devido ao efeito Joule implica o fato de ocorrer um sobredimensionamento nos equipamentos e, assim, tem-se um acréscimo no custo de sua fabricação.
Sabe-se que as perdas em transformadores aumentam proporcionalmente ao aumento da frequência. Dessa maneira, surgem algumas indagações:
• Qual a diferença entre o impacto de uma onda quadrada e uma onda senoidal nas perdas? Ou ainda, entre se ter uma onda quadrada e um somatório de senóides de diversas frequências?
• O problema do aumento das perdas não está relacionado com a taxa de variação da forma de onda da tensão ou da corrente?
• Não é a mudança de sentido do sinal mais frequente que acarreta no acréscimo das perdas? Por exemplo, para as perdas por correntes parasitas, a tensão induzida nas subidas e descidas da onda quadrada corresponde à induzida pelo somatório das induzidas por cada harmônica?
• Se as perdas no transformador aumentam, uma corrente não linear teria de ter valor eficaz maior que uma corrente linear para possibilitar à carga produzir o mesmo trabalho. Mas quanto maior?
Mesmo o transformador apresentando alta imunidade às falhas operacionais, a preocupação com seu constante funcionamento é muito grande, já que uma falha na sua operação pode acarretar uma parada completa de um sistema elétrico. Nesse campo, o estudo aqui presente vem reforçar a prestabilidade das características comportamentais dos transformadores, bem como analisar os possíveis impactos sofridos quando estes alimentam cargas com características não lineares. Para tanto, este artigo apresenta um estudo experimental sobre o comportamento das características elétricas de transformadores suprindo cargas não lineares. As análises são baseadas nas perdas elétricas e energias dissipadas envolvidas.
Perdas em transformadores
Embora o transformador seja um equipamento que apresenta elevado rendimento, não se pode desprezar suas perdas, uma vez que estas são responsáveis pelo seu aquecimento, tornando-se fator limitador da sua capacidade de transferência de potência. Estas perdas podem ser divididas como mostra a Figura 1.
Figura 1 – Divisão das perdas do transformador.
Da Figura 1 pode-se observar que as perdas totais do transformador (PT) são divididas em perdas a vazio (P0) e perdas em carga (PC).
As perdas a vazio, ou perdas no ferro, aparecem por causa do fluxo de magnetização produzido pela tensão aplicada ao transformador. Estas perdas podem ser subdivididas em perdas por histerese magnética (PH), em perdas por correntes parasitas de Foucault no núcleo (PF) e em perdas adicionais (Pad), que são as perdas suplementares no ferro e às dissipações em algumas partes construtivas do transformador. As equações que definem as perdas a vazio são as equações (1), (2) e (3) conforme [1].
Em que PH-0 são as perdas pelo efeito de histerese sem a presença de distorção, em watts, por quilograma de núcleo; KH é um coeficiente que depende do tipo de material usado no núcleo; B é a indução (valor máximo) no núcleo em Wb/m2; ? é o coeficiente de Steimmetz; e f é a frequência em Hz.
Em que PF-0 são as perdas por correntes parasitas sem a presença de distorção, em watts por quilograma de núcleo; f é a frequência em Hz; B é a indução máxima no núcleo em Wb/m2; e d é a espessura da chapa em milímetros. Finalmente, as perdas adicionais são:
Sendo assim, as perdas a vazio sem a presença de distorção está representada pela equação (4).
Por sua vez, as perdas em carga sem a presença de distorção (PC-0) podem ser subdivididas em perdas por efeito Joule (PJ-0) nos enrolamentos primário e secundário, em virtude de resistência elétrica dos enrolamentos, e em perdas adicionais, como consequência do fluxo de dispersão (PFD-0).
Este fluxo é produzido pela corrente de carga nos enrolamentos e irá atravessar o núcleo, o próprio enrolamento e outras partes do transformador, como grampos, tanque, etc. Desta forma, as perdas podem ser divididas em perdas por fluxo de dispersão nos enrolamentos e perdas por fluxo de dispersão nos outros componentes (POFD-0).
As perdas por fluxo de dispersão nos enrolamentos são usualmente chamadas de perdas por correntes parasitas nos enrolamentos (PCP-0), pois o fluxo de dispersão, incidindo no enrolamento dá origem a pequenas correntes em forma de vórtices. A intensidade destas correntes depende do formato e da espessura do enrolamento, da proximidade entre o enrolamento e o núcleo, da corrente de carga elevada ao quadrado e da frequência da corrente também elevada ao quadrado. Assim, as perdas em carga (sem distorção) podem ser definidas pela equação a seguir:
Vejamos agora o comportamento das perdas do transformador adiante da presença de distorções harmônicas de tensão e de corrente.
Efeitos das distorções nas perdas de transformadores
Transformadores são desenvolvidos para transferirem a potência requerida pela carga com as mínimas perdas à frequência fundamental. Desta forma, tensões e correntes distorcidas, por serem possuírem componentes de frequência fundamental e suas múltiplas, contribuem para o aumento das perdas e, por consequência, do aquecimento do transformador. Será feita aqui uma análise do comportamento das perdas a vazio e das perdas em carga nestas situações.
Efeitos da distorção de tensão nas perdas a vazio
Sabe-se que as perdas a vazio são provocadas pelo fluxo de magnetização produzido pela tensão aplicada no lado primário do transformador. Desta maneira, se a tensão aplicada for distorcida, ou seja, apresentar componentes de frequências maiores que a da fundamental, ocorrerá um acréscimo das perdas no núcleo, pois, como visto, as perdas por histerese são proporcionais à frequência, e as perdas por correntes parasitas de Foucault no núcleo são proporcionais ao quadrado da frequência. O quanto tais perdas irão aumentar dependerá do módulo de cada harmônico de tensão associado à ordem harmônica de cada componente. As perda
s por histerese e as perdas por correntes parasitas são obtidas pelas equações (6) e (7) respectivamente.
Tais formulações podem ser encontradas em [2], em que PH é a perda por histerese e PF é a perda por correntes parasitas corrigidas com a distorção presente no sinal de tensão:
Sendo h a ordem harmônica; Vh a tensão do enésimo harmônico; V1 a tensão da fundamental; ?h o ângulo de fase do enésimo harmônico de tensão; e ? o coeficiente de Steimmetz.
Na equação (7), o coeficiente Cen depende da espessura do núcleo (?), da permeabilidade magnética do núcleo (?), da condutividade elétrica do núcleo (?) e da frequência da componente fundamental (f). O valor de Cen é calculado usando as equações de (8) a (10).
Vale ressaltar que, mesmo para sistemas de distribuição, os valores de distorção de tensão não costumam ser muito elevados. Valores em torno de 1% a 5% são comumente encontrados. E, uma vez que a variação das perdas a vazio depende diretamente de quanto a tensão está distorcida, pode-se presumir que as possíveis alterações das perdas a vazio diante da distorção de tensão não serão tão relevantes quanto as possíveis alterações das perdas em carga na distorção de corrente, como será visto adiante.
Efeitos da distorção de corrente nas perdas em carga
As perdas provocadas pela dissipação de energia nas resistências dos enrolamentos, bem como as perdas consequentes do fluxo de dispersão, são sensíveis às variações da corrente de carga. Desta maneira, se a corrente de carga for distorcida,
mantendo-se o valor da fundamental, haverá um acréscimo no seu valor eficaz devido aos harmônicos, provocando, assim, um aumento nas perdas Joule (rI2eficaz). Com a presença de componentes de frequências maiores que a da fundamental, outro efeito que se torna relevante é o efeito pelicular, no qual ocorre uma diminuição da área condutora do condutor e por consequência um aumento de sua resistência, implicando em uma maior dissipação de energia nos enrolamentos.
Outra perda que não pode ser desprezada é aquela causada pelas correntes parasitas nos enrolamentos, a qual aumenta com a elevação da frequência. Esta perda é proporcional ao quadrado da corrente de carga e ao quadrado da frequência, como mostra a equação (11):
Em que FHL é o fator de perda harmônica para correntes parasitas nos enrolamentos. O aumento destas perdas pode causar um aumento excessivo da temperatura dos enrolamentos.
Por fim, as perdas por fluxo de dispersão em outros componentes (grampos, parafusos, carcaça, etc.) apresentam também um acréscimo proporcional à presença de conteúdo harmônico na corrente de carga. A relação entre estas perdas e as harmônicas é mostrada a seguir:
Em que FHL-OFD é o fator de perda harmônica por fluxo de dispersão em outros componentes.
Como se pode observar pelo expoente de h, o acréscimo das perdas em virtude do aumento do conteúdo harmônico é mais expressivo nas perdas por correntes parasitas nos enrolamentos do que nas perdas por fluxo de dispersão em outros componentes. Com este aumento de conteúdo harmônico haverá a necessidade de uma redução no valor máximo da corrente do transformador, devido ao aumento da temperatura nos enrolamentos. Esta redução pode ser avaliada pela equação (13):
Medições laboratoriais
Nesta seção serão apresentados os resultados das medições realizadas no laboratório de eletrotécnica da Universidade Federal de Itajubá. Tais resultados evidenciam os efeitos sofridos por um transformador, quando este é submetido a diferentes situações de carga. Um transformador delta/estrela de 2 kVA foi utilizado nos testes. A Figura 2 mostra a foto do transformador sob análise.
Figura 2 – Transformador sob análise.
• Caso 1 – Comparação carga resistiva e LFCs
Este caso consistiu na obtenção de resultados de potências, distorções e fatores de potência provenientes de medições efetuadas quando o transformador alimentou um conjunto de resistores (cargas lineares) e, posteriormente, um conjunto de LFCs (cargas não lineares). Com a utilização do medidor de grandezas elétricas RMS MARH-21 992, foram obtidos os resultados das componentes harmônicas.
Primeiro buscou-se obter o valor das perdas nominais, por meio de medições em uma situação com um carregamento de 2 kW puramente resistivo (lâmpadas incandescentes). Deste modo, o resultado obtido para as perdas nominais totais do transformador foi 192 W. De posse deste resultado objetivou-se atingir este valor de perdas nominais totais com uma carga não linear, carga esta que foi composta por computadores e lâmpadas fluorescentes compactas (LFCs). A composição harmônica desta carga, bem como os resultados de potência da carga e de perdas totais do transformador, são apresentados na Tabela I.
Tabela I – Resultados da medição do transformador de 2 kVA
|
Valores |
Fase A |
Fase B |
Fase C |
|
I1 [A] |
2,991 |
5,438 |
5,515 |
|
I3 [A] |
2,022 |
2,404 |
1,930 |
|
I5 [A] |
0,884 |
0,495 |
0,615 |
|
I7 [A] |
0,092 |
0,672 |
0,389 |
|
I9 [A] |
0,156 |
0,311 |
0,163 |
|
I11 [A] |
0,106 |
0,191 |
0,127 |
|
I13 [A] |
0,007 |
0,049 |
0,113 |
|
I15 [A] |
0,064 |
0,021 |
0,085 |
|
DHTi [%] |
74,19 |
47,36 |
37,73 |
|
Potência |
|
1602 [W] |
|
|
Perdas |
|
190 [W] |
|
Pode-se observar da tabela acima que, para esta situação de carga, o valor das perdas nominais foi atingido, porém tem-se agora uma potência ativa consumida igual a 1602 W. Em outras palavras, com a não linearidade de carga apresentada na
Tabela I, o transformador é capaz de suprir uma potência igual a 80,1% de sua potência nominal sem ultrapassar suas perdas nominais.
• Caso 2 – Comparação motor trifásico e conversor de frequência
Este caso consistiu na obtenção de resultados do aumento de perdas elétricas no transformador alimentando um motor de indução e, posteriormente, um conversor de frequência, de acordo com o diagrama esquemático da Figura 3.
Figura 3 – Diagrama elétrico para o sistema de medição 2.
Para adequar a tensão fornecida pela bancada (220 V fase-fase) à tensão no primário do transformador (180 V fase-fase), utilizou-se um varivolt. Sua saída alimenta, do lado de baixa tensão, o transformador de 2 kVA.
A saída do transformador pode ser conectada ao motor, dependendo da situação a ser ensaiada, de duas formas: diretamente ou por meio do inversor de frequência de 3 cv mostrado na Figura 4.
Figura 4 – Inversor de frequência.
Assim sendo, seja diretamente conectado ao secundário do transformador, seja conectado ao inversor de frequência, o motor de indução trifásico (MIT) é acionado. Este, mostrado na Figura 5, possui uma potência nominal de 3 cv e tensão de alimentação de 220 V.

Figura 5 – MIT.
Para a execução da medição de temperatura, foi acoplado um termopar no lado interno do enrolamento do transformador e sua saída foi ligada ao transmissor de temperatura que é conectado ao medidor RMS. Assim sendo, para o registro adicional de tensões e correntes foram conectados dois desses medidores, um de cada lado do transformador.
Finalmente, o sistema de medição, completamente montado em laboratório, pode ser observado na Figura 6.
Este sistema de medição foi criado para avaliar o aquecimento do transformador e, assim, possibilitou a realização de variados testes. A primeira situação considera o transformador alimentando o MIT (carga linear) e a segunda situação alimentando o inversor de frequência.
Figura 6 – Sistema completo montado para o caso 2.
Primeira situação
A primeira situação de medição foi obtida por meio da alimentação do MIT diretamente pelo secundário do transformador. Ainda nesta, foi colocada no motor a maior carga possível.
Para tanto, as tensões e as correntes registradas no secundário do transformador durante o processo de aquecimento compõem a curva de tendência mostrada na Figura 7, na qual a cor azul representa a fase A, a cor verde a fase B e a cor vermelha a fase C.
Figura 7 – Curvas de tendência de tensão e corrente para a primeira situação.
Observa-se certo desequilíbrio tanto entre as tensões quanto entre as correntes. Este é devido tanto ao varivolt quanto ao próprio transformador.
Por fim, e mais importante, como mostrado na Figura 8, foi registrada a temperatura no transformador.
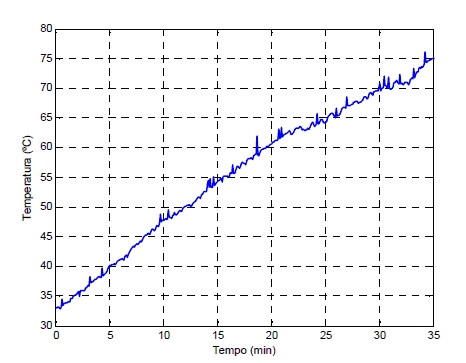
Figura 8 – Curva de aquecimento do transformador para a primeira situação.
Segunda situação
Na segunda situação, colocou-se um inversor de frequência entre o secundário do transformador e o MIT, mantendo-se a condição de carga máxima.
Durante a realização dessa experiência, obtiveram-se as curvas de tendência mostradas na Figura 9.
Figura 9 – Curvas de tendência de tensão e corrente para a segunda situação.
Foram registrados no transformador os valores de temperatura a cada cinco segundos, os quais geraram a curva de aquecimento mostrada na Figura 10.
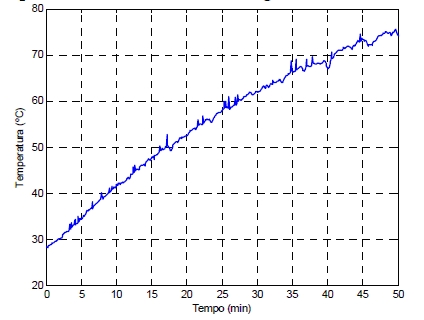
Figura 10 – Curva de aquecimento do transformador para a segunda situação.
Observa-se que o tempo de aquecimento foi de aproximadamente 50 minutos, consideravelmente maior do que o tempo para a situação 1. Este fato ocorreu devido ao valor eficaz da corrente ter diminuído (Figura 8 versus Figura 10) da primeira situação para a segunda situação. Explica-se essa diminuição pelo fato de que, apesar de o inversor consumir uma corrente distorcida, ele também reduz o ângulo de deslocamento entre tensão e corrente aproximadamente de 35º a 14º. Em outras palavras, para esse sistema de medição, quando da inserção do inversor de frequência a corrente eficaz diminui, uma vez que parte considerável de seu módulo era devido ao deslocamento entre tensão e corrente.
Assim sendo, criou-se uma terceira situação em que ocorreu uma diminuição da carga da primeira situação e igualou-se a corrente eficaz não linear da segunda situação com a linear da terceira situação.
Terceira situação
Para a obtenção da terceira situação, a carga do motor foi reduzida de tal maneira a igualar a corrente registrada no secundário do transformador à registrada quando da segunda situação. Ou seja, o objetivo é comparar o aquecimento provocado por uma corrente distorcida diante do provocado por uma corrente senoidal, ambas de mesmo valor eficaz.
Dessa forma, inicialmente são mostradas, na Figura 11, as curvas de tendência dos registros de tensão e corrente.
Figura 11 – Curvas de tendências de tensão e corrente para a terceira situação.
Também, como mais importante objeto de comparação, foi registrada a temperatura do transformador ao longo do processo de aquecimento, curva tal que pode ser visualizada na Figura 12.
Observa-se que o tempo de aquecimento foi maior do que na situação não linear, ou seja, este fato implica que as perdas aumentam na distorção da forma de onda da corrente.
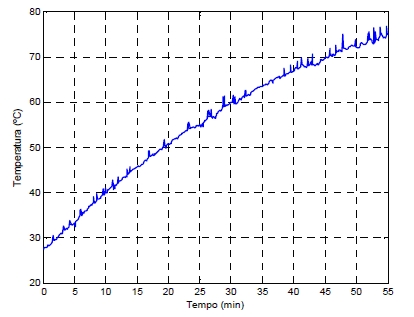
Figura 12 – Curva de aquecimento do transformador para a terceira situação.
Análise comparativa dos aquecimentos
Inicialmente, como mostra a Figura 13, pode-se comparar as curvas de aquecimento obtidas com os ensaios da segunda situação (não linear) e terceira situação (linear).
Figura 13 – Curvas de aquecimento – terceira situação (linear) versus segunda situação (não linear).
Como pode ser notado na Figura 13, existe a dificuldade, devido à instabilidade do transmissor de temperatura, de se trabalhar com os valores adquiridos durante o ensaio, portanto, lança-se mão de técnicas de regressão. Observando a tendência da curva de aquecimento, optou-se por aumentar para 2ª a ordem da regressão, ou seja, resolveu-se trabalhar com um polinômio de ordem 2. Da mesma forma, os resultados gráficos e analíticos são mostrados na Figura 14 e na expressão (14).
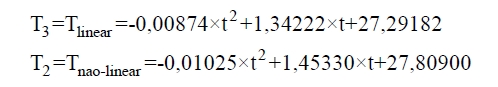
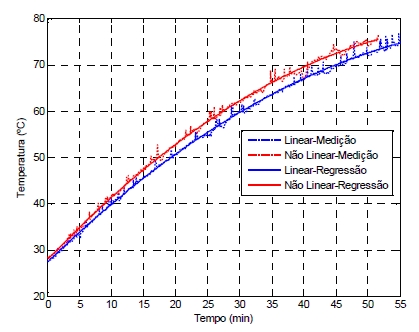
Figura 14 – Regressão polinomial.
Acréscimo de perdas
De posse do comportamento da temperatura em função do tempo para cada uma das duas situações ensaiadas e admitindo-se a temperatura ambiente constante e idêntica durante os ensaios, pode-se estimar as perdas para cada situação da seguinte maneira:
Em que n denota a situação em questão, m a massa do resistor, c o calor específico do mesmo, T1 a temperatura e t o tempo. Admite-se para as duas situações que:
Assim sendo, tem-se, para cada situação, a seguinte relação entre perdas e aquecimento:
No entanto, não faz sentido uma avaliação isolada do quadro obtido quando do ensaio de cada situação, faz sentido sim a avaliação comparativa entre as duas situações em questão, ou seja, situação de linearidade diante da situação de não linearidade. Tal avaliação pode ser feita da seguinte maneira:
Dessa maneira, a comparação das perdas causadas pela corrente da segunda situação (não linear) em relação à corrente da terceira situação (linear) é realizada da seguinte forma:
Avaliando a relação no instante de maior derivada, ou seja, no instante 0, tem-se:
De acordo com esse resultado obteve-se, por meio da medição do aquecimento, que as perdas elétricas do transformador quando da alimentação do inversor são 8,28% maiores do que as perdas quando da alimentação direta do motor.
No entanto, de acordo com a medição da amostra dos sinais de tensão e corrente, obteve-se o resultado de que o transformador sofreu uma sobrecarga de aproximadamente 9,27 %, quando da inserção do inversor, forçando a igualdade das correntes eficazes.
Conclusões
Foi possível observar ao longo deste trabalho que um transformador, com o aumento da não linearidade da carga, pode atingir níveis maiores que os admissíveis de perdas, o que deve levar a uma redução da sua potência máxima disponível. Condição esta que, se não respeitada, pode acarretar na redução do tempo de vida útil do transformador.
Complementarmente, a respeito das medições realizadas no caso 2 observou-se que, quando da utilização de carga máxima, a corrente eficaz fornecida por meio do transformador foi maior para a situação na qual não se utilizava o inversor de frequência. Este fato pode ser justificado de acordo com a capacidade do inversor em elevar o fator de potência de deslocamento praticamente à unidade. Quando da comparação das situações de linearidade e não linearidade para a mesma corrente eficaz, obteve-se uma curva de aquecimento mais acentuada quando da circulação da corrente distorcida. Consequentemente, as perdas obtidas pela situação de não linearidade foram aproximadamente 8% maiores do que as obtidas para a situação de linearidade, mostrando que realmente se deve considerar a diminuição da vida útil de transformadores devido ao maior aquecimento provocado pela alimentação de cargas não lineares.
Referências
[1] OLIVEIRA, J. C.; COGO, J. R.; ABREU, J. P. G. “Transformadores – teoria e ensaios”. 1984.
[2] DELAIBA, A. C.; OLIVEIRA, J. C.; VILAÇA, A. L. A.; CARDOSO, J. R. “The effect of harmonics on power transformers loss of life”. 1996.[3] IEEE Std C57.110-1998. “IEEE Recomended Pratice for Estabilishing Transformer Capability When Supplying Nonsinusoidal Load Currents”, 2008.
[4] MASOUM, M. A. S. ”Derating of anisotropic transformers under nonsinusoidal operating conditions”. IEEE Transactions on Electrical Power Energy System, v. 25, p. 1-12, 2003.
[5] FUCHS E. F.; LIN, D.; MARTYNAITIS, J. “Measurement of threephase transformer derating and reactive power demand under nonlinear loading conditions”. IEEE Transactions on Power Delivery., v. 21, n. 2, p. 665-672, Apr. 2006.
[6] FUCHS E. F., LIN, D., “Real-time monitoring of iron-core and copper losses of transformers under (non)sinusoidal operation”. IEEE Transactions on power delivery, v. 21, n. 3, July 2006.
[7] FUCHS, E. F.; MASOUM, M. A. S. “Power quality in power systems and electrical machines”, 1e, 638 p, Elsevier, USA, March 2008.
* Marcel Fernando da Costa Parentoni é doutorando (nesta linha de pesquisa) e professor na Universidade Federal de Itajubá, campus Itabira-MG;
Fernando Nunes Belchior, Paulo Márcio Silveira, Délvio F. Bernardes são professores na Universidade Federal de Itajubá, campus Itajubá-MG;
Jocélio de Souza Sá é professor aposentado da Unifei, atuando a mais de 25 anos na área de Qualidade da Energia Elétrica;
José Policarpo Gonçalves de Abreu é professor aposentado da Unifei, atuando a mais de 25 anos na área de Qualidade da Energia Elétrica. Atualmente, é Diretor Científico da Fapemig-Fundação de Amparo à Pesquisa do Estado de Minas Gerais;
Francisco J. D. M. Galvão Júnior é formado na Unifei, atuando na Empresa Alstom Brasil Ltda, em Taubaté-SP;
Ivan Paulo Faria é discente do 5º ano na Unifei, Campus Itajubá-MG.