Após apresentar a dedução matemática da expressão da corrente de curto-circuito e suas variantes mais usuais, iremos considerar agora as condições especiais (condições limites) que o sistema elétrico pode apresentar, e verificar como a corrente de curto-circuito se comporta nessas condições. Para esse exame deve ser lembrado que:
Este termo é constante desde que, para um determinado curto-circuito já ocorrido, Em e Z são constantes, λ foi fixado no momento da falta, e ϕ está fixado pela relação X/R.
Observa-se que quando é muito grande, isto é, τ ≈ ∞, o valor de e a componente contínua será igual ao termo constante, equação (6-2). Nota-se também que se λ = ϕ, a componente contínua não existe, pois o termo sen(λ – ϕ) será nulo. Ambos os casos, τ → ∞ e λ = ϕ são mostrados, respectivamente, nas Figuras 5-a e 5-b (para 5 ciclos).
6.1 – Circuito puramente resistivo
Se R >> X, então a relação X/R → 0, e o termo exponencial decrescente tende também a zero, pois na equação (6.3):
Isso significa que a componente contínua é igual a zero e só existe o termo da componente AC simétrica:
Também o ângulo ϕ é igual a zero, pois ϕ = arctg(X/R) = arctg(0°), ou seja, a componente AC está em fase com a tensão. Logo, quando o circuito é puramente resistivo, a corrente de curto-circuito está em fase com a tensão, não existe componente contínua e nem assimetria e a equação (3-2) da corrente de curto se resume a sua componente alternada simétrica. Esse comportamento é ilustrado na Figura 6.
6.2 – Circuito puramente indutivo
Se X >> R, a relação X/R → ∞ e ϕ = arctg(∞) = 90°. Logo, a corrente de curto-circuito está defasada de 90° da tensão.
Conclui-se que a componente contínua, se existir (isto é λ ≠ 90°), será igual ao seu termo constante e nunca decairá. Em outras palavras, a corrente de falta resultante será sempre assimétrica (com exceção de λ = 90°), pois será a soma do termo simétrico mais um termo constante. A Figura 7 mostra esse comportamento.
6.3 – Condição geral
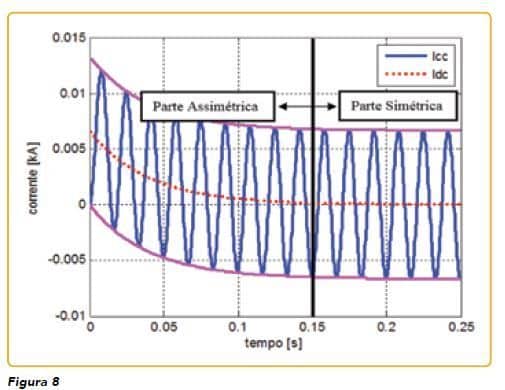
Após a análise das condições anteriores (R >> X e X >> R), que são condições limites, entende-se facilmente a condição em que R e X têm valores diferentes de zero, sendo essa a condição geral. A forma de onda da corrente apresentará tanto a componente AC permanente simétrica, como a componente DC (exponencial decrescente). A forma de onda será como na Figura 8.
6.4 – Condição geral de plena simetria
Vimos que, em sistemas puramente resistivos ( R >> X ), a componente contínua é nula e a corrente de curto-circuito é sempre simétrica, conforme equação (6-5). E para um sistema qualquer? É possível que a corrente de curto-circuito seja simétrica? Sabemos que o ângulo λ é definido no momento de ocorrência do curto-circuito. Pela expressão da componente DC, equação (3-2), verifica-se que:
Portanto, na situação anterior, a componente contínua desaparece na fase e a corrente de curto-circuito resultante será simétrica. Observa-se que, no sistema trifásico, pelo defasamento angular de 120° entre as correntes, só existe a possibilidade de plena simetria da corrente de curto-circuito em uma fase.
A equação (6-9) é importante, pois mostra que para qualquer sistema, isto é para qualquer X/R , é possível ter a corrente de curto simétrica. Se o sistema é indutivo, X >> R, condição de sistemas de potência (SEP), ϕ ≈ 90° e para que haja somente a corrente AC simétrica a corrente de curto deve se iniciar obrigatoriamente no momento que a tensão passa pelo máximo (λ = 90°). Esse comportamento pode ser visto na Figura 9.
6.5 – Condição de máxima assimetria
Entende-se como condição de máxima assimetria aquela condição do sistema elétrico que produz o maior valor possível de componente contínua, no curto-circuito. Esta condição pode ser obtida da análise da componente contínua:
Como se trata de uma exponencial decrescente com o tempo, multiplicada por uma função seno com sinal negativo bem como multiplicada por um termo constante Im, o máximo da função dc(t) ocorrerá quando forem atendidas simultaneamente as seguintes condições:
O sinal positivo significa que a componente DC está no primeiro quadrante dos eixos cartesianos, fato que ocorrerá somente quando a onda de tensão, passando por zero em ω.t = –λ = –(ϕ – π/2) = π/2 – ϕ, cresce na direção positiva do eixo das ordenadas, conforme Figura 10-a.
O sinal negativo significa que a componente DC está no quarto quadrante, o que ocorre quando a onda de tensão passando for zero em ω.t = –λ = –(ϕ – π/2) cresce na direção negativa do eixo das ordenadas, conforme Figura 10-b.
Portanto, podemos resumir, afirmando que a componente contínua apresenta o seu valor máximo possível no instante t = 0 (momento de ocorrência do curto), e quando λ = ϕ ± π/2, concluindo ainda que o seu valor máximo é igual ao valor de pico da componente AC simétrica.
Para sistemas indutivos (X >> R), condição de sistemas de potência (SEP), ϕ = 90°, λ = ϕ – 90° = 0°. Isto significa que a máxima assimetria ocorrerá quando a tensão estiver passando por zero, no momento do curto. Observa-se ainda que, levando-se em conta a condição de máxima assimetria, a expressão geral da corrente i(t) se tornará:
Esta relação é importantíssima para analisar a saturação dos transformadores de corrente, pois a pior condição de saturação ocorre na condição de máxima assimetria, isto é, maior presença possível da componente contínua.
6.6 – Determinação do tempo para a corrente de curto-circuito atingir o valor de pico
Em um sistema elétrico existente (onde são conhecidos Emax, Z, f e f), o valor de pico da corrente de curto-circuito só depende do valor inicial do ângulo l (l = l0), e ocorrerá em um certo tempo t (t = tp).
Para cada valor de l = l0 existirá um valor de t = tp, no qual a corrente atinge o valor de pico (Figura 11).
O valor de tp pode ser determinado inserindo-se λ = λ0 na equação geral, equação (3-2), ou qualquer de suas variantes, derivando-se a referida equação em relação a t e igualando-se o resultado a zero. Com este procedimento, o valor de tp encontrado será:
Considerando que, para um sistema de potência, ϕ ≈ π/2, os valores de tp para as condições de máxima assimetria, condição de plena simetria e condição parcial de assimetria valem respectivamente:
Esta condição é impossível fisicamente, pois a corrente não pode alcançar o seu valor máximo instantaneamente (t = 0) em um circuito indutivo. A Figura 12-a mostra a curva da corrente de curto-circuito para a máxima assimetria, a Figura 12-b mostra a onda de tensão e corrente no mesmo sistema de eixos, o valor de λo = π é que provoca a máxima assimetria uma vez que X >> R e, consequentemente, ϕ ≈ π/2.
Variando-se λ e mantendo-se fixo o valor de X/R, conclui-se que o tempo tp no qual ocorre o valor de pico da corrente de curto-circuito, situa-se teoricamente entre tp = 0 ciclo e tp = ½ ciclo.
6.7 – Determinação do valor de pico da corrente de curto-circuito
Com os parâmetros do sistema definidos, e para um dado λ = λ0, a equação (6-18) permite calcular o valor do tempo tp no qual ocorrerá o valor de pico da corrente de curto-circuito.
Para determinar o valor de pico da corrente do curto trifásica resultante (isto é, considerando-se a soma das componentes AC e DC) basta entrar com λ = λ0 e t = tp em qualquer uma das equações gerais, por exemplo a equação (3-2), obtendo-se então:
6.8 – Fator de assimetria
A relação entre o valor de pico da corrente de curto-circuito e o valor eficaz da componente simétrica senoidal é denominado “fator de assimetria”, conforme equação abaixo:
Este fator pode ser obtido das equações (3-13), (4-3) e suas variantes, apenas introduzindo λ = λ0 e t = tp nas mesmas. Por exemplo, a partir da equação (3-13), onde o tempo está em segundos:
Considerando f=60Hz e um sistema de potência tal que ϕ ≈ π/2 e X/R ≈ ∞, a tabela a seguir mostra os valores de Kassim, obtidos da equação (6-25) para as condições de máxima assimetria, condição de plena simetria e uma condição parcial de assimetria, situações vistas no item 6.6.
Observa-se que considerar ϕ ≈ π/2 para SEP é muito conservativo, elevando o valor de Kassim.. Uma situação mais real seria considerar, por exemplo, o SEP com uma constante de tempo em torno de 0,1 segundo. Nesta condição, temos da equação (3-15), onde τ está em segundos;
Mantendo-se os valores de λ0 e tp da tabela 6-1, os valores de Kassim para as condições de máxima assimetria e assimetria parcial, seriam respectivamente:
6.9 – Condição para ocorrer o valor máximo de pico (Ipm) da corrente de curto
Chamamos de valor máximo, ou valor de pico da corrente de curto-circuito trifásica, o valor instantâneo máximo medido na onda resultante da corrente, considerada sua expressão geral (presença simultânea da componente AC e da componente DC).
A componente contínua, que define a assimetria, depende do ângulo λ. Dessa forma, verifica-se que um dado sistema com X/R definido, apresentará um valor de pico para cada λ. Assim, existirá um valor l = lpm para o qual o valor de pico será máximo.
Chamaremos esse valor de pico de Ipm para diferenciar do valor de pico Im da componente alternada simétrica, bem como do valor de pico Ip que ocorre para um λ qualquer, isto é λ = λ0 que não produz o valor Ipm. O valor de Ip para um determinado λ = λ0 qualquer é dado pela equação (6-23) ou uma de suas equivalentes. Derivando-se no tempo a equação geral e igualando o resultado a zero, mostra-se que a condição para ocorrer o valor máximo de pico Ipm, é:
Verifica-se que, quando λpm = 180° a corrente de curto é a “imagem espelho” da condição λpm = 0°, isto é, a componente contínua está no quarto quadrante ao invés de estar no primeiro quadrante, e o valor de pico da corrente assimétrica resultante é negativo ao invés de positivo. Em todas as considerações a seguir, o valor de λ para a condição de máximo de pico Ipm será λpm = 0°
Conclui-se, pois, que a condição de máximo pico Ipm, isto é (λpm = 0), difere da condição de máxima assimetria λ = ϕ + π/2 ou λ = ϕ – π/2.
7. Comparação das condições de máxima assimetria e máximo pico
Vimos que as condições de ocorrência de máxima assimetria e máximo pico são diferentes. É interessante comparar os parâmetros mais importantes da corrente de curto-circuito para essas duas situações. A tabela 7.1 mostra os principais parâmetros da corrente de curto-circuito, avaliados para diferentes valores de X/R na condição de máximo valor de pico (λ = λpm = 0) e o tempo para ocorrer este valor de pico, (tempo tpm dado em ciclos)
Observa-se na tabela 7.1 que o tempo para o qual ocorre o valor máximo de pico (tpm), varia com o valor de X/R, variando de 0,26 ciclos para X/R = 0,1 até 0,5 ciclo para X/R = 1000. O valor máximo de pico, em p.u, da corrente simétrica varia de 1 para X/R = 0,1 até 2 para X/R = 1000. A tabela 7.2 compara os valores de pico para condição de máxima assimetria com valores de pico para a condição de máximo valor de pico, para diferentes valores de (X/R).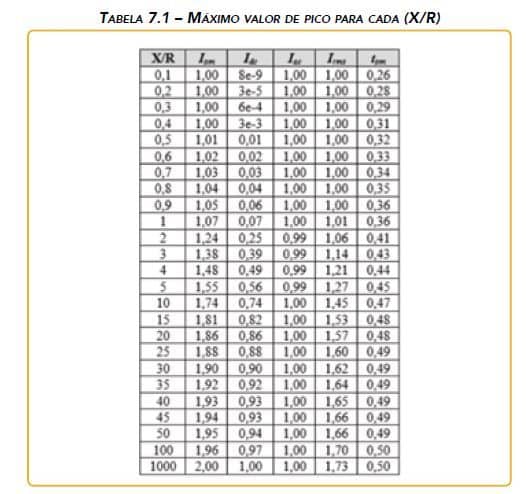
Para a tabela 7.1, tem-se:
Ipm – Máximo valor de pico da corrente para cada X/R, em p.u do valor de pico da corrente simétrica (λpm = 0, t = tpm);
Idc – Valor máximo da componente DC, em p.u do valor de pico da corrente simétrica (λpm = 0, t = tpm);
Iac – Valor instantâneo da componente AC, em p.u do valor de pico da corrente simétrica (λpm = 0, t = tpm);
Irms – corrente rms resultante (assimétrica), em p.u, do valor de pico da corrente simétrica (λpm = 0, t = tpm);
tpm – tempo para Ipm ocorrer em ciclos.
Para a tabela 7.2, tem-se:
Ip-ma – (máxima assimetria) – corrente de pico conforme condições de máxima assimetria (λ0 = ϕ ± π/2; t = tp);
Ip-mp – (máximo pico) – máxima corrente de pico possível (Ipm) (λ0 = λpm = 0; t = tpm);
Irms – (máxima assimetria) – corrente eficaz conforme condições de máxima assimetria (λ0 = ϕ ± π/2; t = tp);
Irms – (máximo pico) – corrente eficaz conforme condições de corrente de pico máxima (λ0 = λpm = 0; t = tpm);
Irms – corrente eficaz calculada sobre o 1º ciclo, em condições de máxima assimetria (λ0 = ϕ ± π/2; t = 0,0167s = 1 ciclo).
Observa-se que as diferenças percentuais entre os valores de pico para a condição de máxima assimetria (Ip-ma) e os valores de pico para a condição de máximo pico (Ipm) são relativamente pequenas, atingindo, no máximo, 2,75% para X/R=2. Para valores de X/R > 15, os dois valores são praticamente iguais.
Com esta observação, e considerando também a tabela 7.1 que para valores de X/R > 5 o tempo para ocorrer o valor máximo de pico (Ipm) é praticamente igual a 0,5 (meio) ciclo, podemos formar um critério simples de calcular o próprio valor máximo de pico (Ipm), como indicado a seguir.
8. Determinação simplificada do valor máximo de pico (Ipm)
O valor máximo de pico (Ipm) da corrente resultante de curto-circuito pode naturalmente ser obtido derivando a equação geral, (3-2). Deve ser verificado que, definido o local de cálculo de curto-circuito do sistema, os valores de X/R, f (frequência) e ϕ = arctg(X/R) são previamente conhecidos.
A equação geral se torna então função de λ e t. Portanto, o valor máximo de pico ocorrerá para um dado valor apropriado de λ = λpm e um dado valor apropriado de t = tpm , isto é: Ipm = f(λpm , tpm)
A determinação de Ipm derivando a equação geral (3-2) ou qualquer de suas equivalentes já vista, é trabalhosa, envolvendo derivadas parciais. Uma primeira conclusão importante derivando em relação a λ, nos leva à equação (6-26), isto é, o valor máximo de pico ocorre para λ = λpm = 0.
A partir daí, para calcular o valor de Ipm, seria necessário antes determinar o valor do tempo para o qual o mesmo ocorre (tpm), o que pode ser realizado utilizando a equação (6-18).
Após determinarmos tpm, teríamos de voltar a equação (3-2) e introduzir λpm = 0 e o valor de tpm, calculando então o valor final de Ipm.
No entanto, podemos evitar todo este trabalho, aproveitando as conclusões do item anterior, ou seja:
Logo, para calcular Ipm, supomos a condição de máxima assimetria (λ = ϕ ± π/2) e o tempo de 0,5 ciclo. Se escrevermos a equação (3-2) da seguinte forma, com o tempo em ciclos, e em p.u do valor máximo da componente:
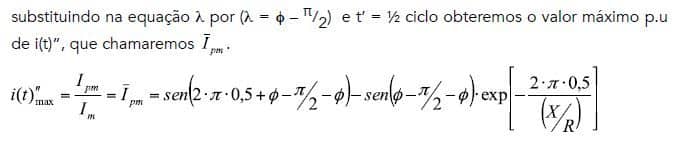
O valor de na equação (8-2) está em p.u do valor de Im (valor de pico da componente simétrica). Se Im =. Irms, estiver em Ampéres, podemos obter os valores de Ipm em Ampéres com as seguintes equações:
Deve ser lembrado que as fórmulas (8-2) a (8-4) são utilizadas com maior precisão para o coeficiente X/R > 5. Quando for necessária uma precisão maior ainda, poderá ser utilizado o procedimento geral de encontrar tpm através da equação (6-18) fazendo λ0 = λpm = 0 e em seguida entrar com o valor encontrado de tpm na equação (6-23) ou outra equação geral, determinando finalmente o valor de Ipm. As equações (6-18) e (6-23) ficam conforme a seguir:
Observe que, nestas equações, tpm está em segundos. Para o tempo em ciclos, utiliza-se as relações (4-1) e (4-2), isto é:
A equação (8-6) ficará:
A partir do momento que a bobina de abertura de um disjuntor é energizada com sua tensão nominal, através da operação de um relé de proteção por exemplo, é despendido um certo tempo para que os seus contatos se separem inteiramente, e então a corrente de curto-circuito seja extinta na sua passagem subsequente por zero. O tempo de separação de contatos é indicado pelo fabricante em ciclos, podendo variar em geral de 1.0 a 3,0 ciclos conforme a tecnologia do disjuntor. Considerando que um relé de proteção rápido opera em cerca de meio (0,5) ciclo, a separação de contatos completa ocorrerá entre 1,5 a 3,5 ciclos.
Neste tempo, considerando os valores de X/R normais dos sistemas de potência, a corrente de curto é ainda assimétrica, pois a componente contínua ainda não desapareceu. Naturalmente, o maior percentual da componente contínua aparecerá nas condições de máxima assimetria, e para valores de X/R elevados.
Os disjuntores são dimensionados para abrir uma certa corrente eficaz (Irms), sob um certo valor de X/R. Para a norma ANSI, X/R = 15 e na NBR / IEC, X/R = 17.
Como determinar o valor eficaz da corrente que o disjuntor irá abrir, se neste momento existem duas componentes, uma alternada simétrica (AC) e outra contínua (DC), isto é, a corrente de abertura é assimétrica.
Sabe-se que o valor eficaz desta corrente assimétrica é calculado pela expressão:
dc(t) = valor instantâneo da componente contínua no momento da abertura (final da separação de contatos), considerando a condição de máxima assimetria (λ = ϕ – π/2)
A equação (9-1) pode ser colocada em p.u do valor eficaz da componente alternada simétrica (Irms)
Porém, da equação (6-10), considerando as condições de máxima assimetria, segue que:
Considerando-se o valor de dc(t) em percentual de Im, segue a expressão bastante utilizada para o cálculo do valor da corrente de abertura dos disjuntores:
Substituindo pelo seu valor da equação (9-6) resulta:
As equações (9-9) e (9-10) são importantíssimas, pois fornecem o valor eficaz da corrente assimétrica de abertura dos disjuntores. Na equação (9-10), o valor eficaz da corrente assimétrica está em função do valor eficaz da componente simétrica AC (Irms) do tempo em ciclos (t’) e do valor X/R.
Na equação (9-11), a corrente está somente em função do valor eficaz da componente simétrica AC (Irms) e do percentual [dc(t)%] da componente contínua em relação ao valor de pico da componente simétrica (Im), no momento da abertura do disjuntor.
é denominado fator de capacidade dos disjuntores na norma ANSI, sendo designado pela letra S.
O fator S permite também calcular o valor Irms da corrente assimétrica para qualquer outra aplicação, como por exemplo, para ajustar relés instantâneos eletromecânicos que, em geral, operam na faixa de 0,5 (meio) ciclo a 3 (três) ciclos. Na literatura inglesa, o fator S é chamado também de “fator de multiplicação para decaimento da componente continua” (DC Decrement Multiplying Factor) ou simplesmente “fator de multiplicação”, (Multiplying Factor).
Neste trabalho procurou-se esclarecer diversos aspectos importantes relativos ao comportamento da corrente de curto-circuito trifásico em um sistema elétrico. Considerou-se o curto-circuito “quilométrico”, onde o valor da reatância é constante ao longo do tempo. O caso do curto com “Fonte Local”, próximo a máquinas rotativas, onde a reatância é variável ao longo do tempo será objeto de outro trabalho. Os autores recomendam a leitura da bibliografia indicada para ampliação do conhecimento aqui adquirido.
Referências bibliográficas