Caderno Renováveis – Janeiro de 2017
Uma breve avaliação dos impactos técnicos e econômicos
Por Selma Oliveira, Núbia Brito, Maurício Correa, Benemar de Souza e Rivanildo Soares*
O uso crescente de aparatos tecnológicos, com processos de controle cada vez mais sofisticados e sensíveis à qualidade da energia elétrica, associado à demanda crescente por energia elétrica, à preservação do meio ambiente e à escassez de água, evidencia a necessidade de se agregar fontes renováveis à matriz energética do país, o que representa um dos grandes desafios da sociedade moderna: a sustentabilidade energética. Dentre as fontes renováveis, destaca-se aqui a solar fotovoltaica, que ainda é muito pouco explorada no Brasil.
Dados o seu grande potencial e a necessidade de diversificação da matriz energética mundial, o estudo dos impactos da inserção deste tipo de geração no Sistema de Distribuição de Energia Elétrica (SDEE) constitui atualmente uma área de pesquisa efervescente. De um modo geral, a inserção de qualquer equipamento ou elemento ao SDEE pode gerar impactos positivos e/ou negativos. Esse fato aplica-se também à inserção de geradores distribuídos, cujos impactos são maiores quando o número de geradores cresce. Além disso, tais impactos dependem da configuração e das características do sistema elétrico e dos locais de conexão dos geradores. Dentre os diversos impactos resultantes, destacam-se aqui as variações nos níveis de tensão e nas perdas variáveis na condição de operação em regime permanente.
É fato que a Geração Solar Fotovoltaica (GSF) pode contribuir positivamente na minimização dos problemas relacionados com variações de tensão, entretanto, o monitoramento dos limites permissíveis de tensão é necessário, visto que que a ocorrência de fluxo reverso pode provocar elevação da tensão no ponto de conexão da GSF com o SDEE. Quanto às perdas técnicas, o fato de elas serem diretamente proporcionais ao nível de carregamento do sistema, a presença de GSF próximo à carga pode contribuir para minimizá-las, uma vez que o fornecimento de potência ativa à carga por parte da GSF reduz a corrente da subestação ao ponto de conexão.
A análise do estado da arte atual mostrou que a maioria dos estudos contempla a inserção em pequena escala e conectada ao sistema secundário. Este trabalho apresenta um estudo dos impactos gerados pela conexão de uma usina de GSF no sistema primário. Para isso, fez-se uso de métodos consolidados para obtenção do estado da rede, considerando níveis de penetração da GSF e de patamares de carga diversos, visando a avaliação dos níveis de tensão e de perdas elétricas em um sistema teste. O estudo foi concluído com uma análise de custos visando o cálculo da estimativa do tempo de recuperação do capital investido e de viabilidade do projeto de implantação de uma usina solar fotovoltaica.
Formulação do problema
A formulação do problema foi feita segundo as etapas apresentadas a seguir.
Como sistema teste, utilizou-se um sistema baseado em um alimentador real e, para formulação do modelo do SDEE, consideraram-se: sistema trifásico radial e balanceado, linhas de distribuição representadas por resistência e reatância série, alimentador primário dividido em trechos, os quais são limitados por nós ou barras, sendo cada nó representando um ponto em que pode estar instalado um transformador de distribuição, existir uma bifurcação ou ocorrer mudança de bitola.
Um trecho de alimentador é esquematizado na Figura 1, em que se considerou cada trecho como sendo formado pelo ramo correspondente juntamente com o seu nó terminal.
Figura 1 – Trecho de um alimentador radial monofásico.
Em relação ao modelo de carga, selecionou-se o tipo potência constante, visto que é o mais utilizado em estudos de fluxo de carga e se adequa bem quando se utiliza curva de duração de carga segmentada. Soma-se a isso a sua facilidade de cálculo e implementação computacional.
O levantamento da curva de carga foi feito considerando medição realizada em intervalos de cinco minutos, resultando na curva de carga diária, que, posteriormente, foi segmentada. O procedimento de segmentação é normalmente realizado considerando um número de intervalos pré-definidos, nos quais a carga é considerada constante. Tais intervalos equivalem a patamares de carga e representam níveis distintos, sendo o número de níveis definido conforme o tipo de aplicação e o grau de precisão desejado e, para sua implementação, requer o uso de técnicas de otimização numérica. Neste trabalho, optou-se pela segmentação em três níveis, que representam cargas leve, média e pesada. Para isso, empregou-se uma rotina computacional para segmentar curvas de carga, baseada em algoritmo genético elaborada por [9].
Para o cálculo do fluxo de carga, considerado uma das etapas mais importantes nos estudos relacionados aos sistemas de potência, utilizou-se um método de varredura do tipo backward-forward, atualmente, o mais utilizado para SDEE. Especificamente, empregou-se o Método da Soma das Potências (MSP) proposto por [11], o qual tem formulação matemática simples, é robusto, converge rapidamente e se aplica a sistemas monofásicos ou trifásicos, desde que tenha configuração radial.
O problema de fluxo de carga via MSP consiste em resolver, para cada trecho do alimentador, uma equação biquadrada mediante a qual se relacionam o fluxo de potência em seu final e as tensões nos extremos do trecho. O fluxo de potência no final de um trecho corresponde à carga instalada na barra do trecho mais a soma das potências instaladas e das perdas à jusante. Daí o nome do método, que é interativo nas variáveis perdas. A estimativa inicial é de perdas nulas e a cada interação seus valores são corrigidos até que essas correções deixem de ser significativas.
Ao final da análise extrai-se o seguinte equacionamento:
Em que:
?? ? ?? são, respectivamente, o fluxo de potência ativa e reativa no fim do trecho i;
??? ? ??? são, respectivamente, a cargas ativas e reativas instaladas no fim do trecho i;
Δ?? ? Δ?? são, respectivamente, as perdas ativa e reativa no fim do trecho k;
Ω? é o conjunto de todos os trechos que derivam do trecho i.
O algoritmo de solução pode ser resumido da seguinte maneira:
Análise econômica
Para realizar o estudo de viabilidade econômica e de rentabilidade das alternativas de investimento, foram avaliados os seguintes métodos: Método do Valor Presente Líquido (VPL), Método da Taxa Interna de Retorno (TIR) e Payback.
O VPL tem como objetivo calcular o impacto dos eventos futuros associados a um projeto de investimento em relação ao valor presente, ou seja, calcula o valor presente dos fluxos de caixa gerados pelo projeto ao longo de sua vida útil. Matematicamente, o VLP é simplesmente a diferença entre os aditamentos gerados pelo projeto e os custos associados a ele:
Em que:
I o investimento inicial;
??? o fluxo de caixa do projeto no período de tempo t;
r a taxa de desconto e n, o horizonte de análise do fluxo de caixa. O critério de decisão será positivo quando seu valor for maior que zero.
O TIR tem como objetivo encontrar uma taxa intrínseca de rendimento. Segundo [12], trata-se de uma taxa de retorno do investimento, ou seja, é o valor de i* que satisfaz:
O projeto é economicamente viável se i* for maior que a taxa mínima de atratividade aplicada.
O Payback ou tempo de retorno sobre o investimento é caracterizado pelo número de períodos (tempo) necessário para que o projeto se pague. Ele pode ser computado, conforme [12], por:
Em que: K é a taxa de desconto (igual ao custo de capital do empreendimento); e T o tempo necessário para que o projeto se pague, ou seja, o Payback.
Metodologia
A metodologia desenvolvida para o estudo realizado é apresentada de forma resumida na Figura 2 e baseou-se nos critérios estabelecidos pelos órgãos reguladores. Considerou-se o sistema teste apresentado na Figura 3 (extraído de [13]), que representa um alimentador de distribuição da Companhia Energética da Borborema (Celb), atualmente, Energisa Borborema, suprido pela subestação Bela Vista, situada na cidade de Campina Grande, na Paraíba. O sistema teste possuía aproximadamente 14,5 km de extensão, 103 barramentos e atendia a uma área predominantemente residencial.
No sistema teste foram inseridos geradores fotovoltaicos em alguns barramentos e avaliados diferentes níveis de penetração fotovoltaica (ou seja, diferentes níveis de geração fotovoltaica) e de patamares de carga, o que resultou em diversos cenários, conforme mostrado na Tabela I.
O critério para definição dos pontos de instalação e distribuição dos geradores fotovoltaicos foi realizado por meio da inspeção visual do perfil de tensão do sistema, após análise de fluxo de carga, sem levar em consideração as curvas de cargas. Foram avaliados no perfil de tensão os pontos de maior queda de tensão, os quais foram selecionados para alocar os geradores fotovoltaicos.
O estudo consistiu em avaliar os impactos no perfil de tensão e nas perdas de potência em diversos cenários de penetração fotovoltaica. O estudo foi concluído com uma análise de custos, visando cálculo da estimativa do prazo de recuperação do capital investido.
Figura 2 – Fluxograma da metodologia proposta.
Figura 3 – Diagrama unifilar do sistema teste.
O modelo de gerador fotovoltaico proposto foi utilizado por [14], segundo o qual, a potência de saída, sob dadas irradiância e temperatura, é a seguinte:
Em que: ????, ??, ??, ?, ??e ???? são, respectivamente: a potência máxima de saída do módulo fotovoltaico (250W), o coeficiente de temperatura (%/ºC), o desvio de temperatura (ºC), o rendimento do inversor (0,96), a irradiância no módulo PV (W/m²) e a irradiância nominal (1000W/m²). A temperatura foi considerada constante.
Os dados de irradiância da geração fotovoltaica, obtidos com a segmentação da curva de duração de carga, conforme mostrado nas Figuras 4 e 5, constituem a entrada para a variável ?? do modelo da Equação (8). A resposta do modelo é alocada dentre os dados de potência ativa de entrada, nos barramentos de alocação do GF, para execução do MSP.
Figura 4 – Curva de duração de carga do sistema-teste proposto.
Figura 5 – Curva de duração de irradiância média global proposta.
Análise dos resultados
A avaliação da variação dos níveis de tensão do sistema baseou-se nos limites permissíveis de tensão determinados pela Agência Nacional de Energia Elétrica (Aneel), no módulo 8 do Prodist, que considera uma faixa de variação de ±5%.
Para avaliação do efeito da geração fotovoltaica, tomou-se como referência o caso do alimentador sem conexão dos geradores fotovoltaicos e operando em seu pior cenário (situação de carga pesada sem geração fotovoltaica), denominado aqui de caso base.
A título de comparação e melhor visualização, optou-se pela exibição dos resultados apenas para os barramentos críticos, ou seja, barramentos de maior regulação, que são: barramentos terminais, barramentos de conexão de grandes ramais e barramentos de conexão dos geradores fotovoltaicos. Os valores de tensão nesses barramentos são fornecidos em valor por unidade (pu) e apresentados nas Figuras 6 a 8.
Figura 6 – Tensões resultantes nos barramentos de maior regulação do sistema-teste com GSF instalada nos barramentos 31 e 54.
Figura 7 – Tensões resultantes nos barramentos de maior regulação do sistema-teste para GSF instalada nos barramentos 23 e 92.
Figura 8 Tensões resultantes nos barramentos de maior regulação do sistema-teste para GSF instalada nos barramentos 31 e 92.
Os resultados do cálculo do fluxo de carga em todos os casos estudados, os quais estão especificados na Tabela I, foram conforme o esperado, pois a tensão elevou-se em todos os cenários e barramentos, independentemente do nível de penetração da GSF. Para os cenários exibidos nas Fig. 6 a 8:
Os resultados referentes às perdas técnicas totais são apresentados nas Tabelas II, III e IV. Elas foram calculadas via método da soma de potência, fazendo-se uso das Eqs. (3) e (4). Os cenários com menores valores de perdas estão destacados em negrito. Análise dos resultados mostrou:
O gráfico de barras das perdas de energia calculadas para todos os cenários e configurações avaliadas é apresentado na Fig. 9, que foram calculadas como sendo a estimativa do valor da energia anual economizada considerando a redução das perdas. A tarifa atual para a classe consumidora B1 residencial de baixa tensão, monofásico 220/127 V adotada pela Energiza/Paraíba é de 0,2898 R$/KWh. A perda de energia é obtida fazendo-se uso da perda de energia diária calculada pelo MSP e orçada com base na curva de carga diária, donde extrai-se posteriormente seu equivalente anual.
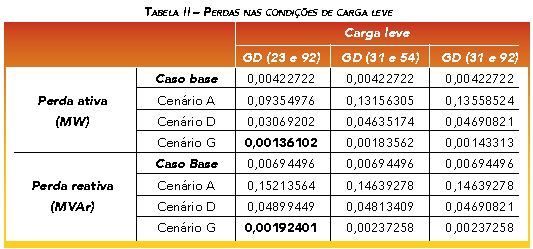
Figura 9- Gráficos de barra de perdas de energia calculadas para todos os cenários estudados
Em relação ao estudo de análise econômica, é importante destacar que essa etapa foi realizada sob a ótica do produtor de energia, com base em um projeto de uma usina solar fotovoltaica de 3 MWp, composta por aproximadamente, 19.400 módulos fotovoltaicos de 250 MWp. O modelo tomado como base foi o proposto por [16] e apresenta os seguintes parâmetros adaptados:
O estudo não contemplou as taxas de juros que possam serem eventualmente aplicadas e os custos associados à depreciação dos módulos e equipamentos que constituem a usina em questão.
Os dados do PLD médio foram extraídos de [17] e a taxa considerada baseou-se na SELIC (Taxa Básica). Os resultados obtidos são apresentados na Tabela V, dos quais se pode concluir:
CONCLUSÕES
Corroborando a literatura especializada, a geração fotovoltaica constitui uma alternativa promissora para atuação conjunta com o sistema elétrico interligado brasileiro. A injeção de potência ativa resultante da conexão desse tipo de fonte ao sistema primário provocou elevação das tensões em todos os barramentos do sistema para todos os cenários avaliados.
Na condição de baixa penetração fotovoltaica, observou-se que sua influência é pequena, entretanto, quando instalados em determinadas condições, a geração solar fotovoltaica pode promover impactos positivos, tanto nos níveis de tensão, quanto na minimização das perdas técnicas e de energia.
Do estudo realizado, verificou-se que cenários que combinem carga máxima com penetração fotovoltaica média (cenário F) tendem a ser muito atrativos para a redução do uso de equipamentos reguladores de tensão e também, para a melhoria geral da qualidade da energia fornecida.
A avaliação econômica realizada demonstrou o quão sensível é a implementação de empreendimentos para geração solar fotovoltaica às taxas vigentes e aplicáveis no Brasil e o quão pouco atrativos ainda são tais projetos, do ponto de vista econômico-financeiro.
Ao final, contatou-se que a metodologia implementada é simples e eficaz na avaliação do comportamento da rede, sem exigir modificações significativas nas ferramentas existentes.
REFERÊNCIAS
[1] L. D. M. Guedes, “Localização e dimensionamento de unidades de geração distribuída em redes de distribuição radiais”, Tese de Doutorado, Universidade de Brasília, 2006.
[2]T. Chang, “Impact of distributed generation on distribution feeder protection”, Doctoral Thesis, University of Toronto, 2010.
[3] T. C. D. C. Fernandes, “Aplicação de técnicas de estimação modal para análise da estabilidade a pequenas perturbações de sistemas de distribuição com geração distribuída”, Tese de Doutorado, Universidade de São Paulo, 2012.
[4] R. A. Shayani, ”Método para determinação do limite de penetração da geração distribuída fotovoltaica em redes radiais de distribuição”, Tese de Doutorado, Universidade de Brasília, 2010.
[5] M. P. S. Martins, ”Inovação tecnológica e eficiência energética”, Monografia de Pós-Graduação, Instituto de Economia-UFRJ, 1999.
[6] L. N. Padilha, “Análise comparativa de estratégias para regulação de tensão em sistemas de distribuição de energia elétrica na presença de geradores distribuídos”, Tese de Doutorado, Universidade de São Paulo, 2010.
[7] J. A. Paludo, ”Avaliação dos impactos de elevados níveis de penetração da geração fotovoltaica no desempenho de sistemas de distribuição de energia elétrica em regime permanente”, Dissertação de Mestrado, Universidade de São Paulo, 2014.
[8] M. M. Frigo, “Impacto da microgeração de energia elétrica em sistemas de distribuição de baixa tensão”, Dissertação de Mestrado, Universidade Federal do Mato Grosso do Sul, 2013.
[9] H. Ferreira, ”Sistemas de distribuição de energia elétrica: um algoritmo genético para alocação ótima de capacitores” Dissertação de Mestrado, Universidade Federal de Campina Grande, julho, 2002.
[10] D. Shirmohammadi, H. W. Hong, A. Semlyen and G. X. Luo, “A compensation-based power flow method for weakly meshed distribution and transmission networks,” IEEE Transactions on Power Systems, v. 3, n. 2, p. 753-762, 1988.
[11] R. P. Broadwater, A. Chandrasekaran, C. T. Huddleston and A. H. Khan, “Power flow analysis of unbalanced multiphase radial distribution systems”, Electric Power Systems Research, v. 14, n. 1, p. 23-33, 1988.
[12] C. P. Samanez, ”Engenharia Econômica, ” Editora: São Paulo, 2009.
[13] B. A. de Souza, H. A. Ferreira, R. J. A. Loureiro, L. F. Cavalcanti, & S. Lima, “Segmentação ótima da curva de duração de carga anual”, Congresso Internacional de Distribuição Elétrica (CIRED), 2002
[14] T. Yao, Y. Tang, and R. Ayyanar, “High resolution output power estimation of large-scale distributed PV systems”, IEEE In Energy Conversion Congress and Exposition (ECCE), 2014.
[15] ANEEL, “Procedimentos de Distribuição de Energia Elétrica – PRODIST, Módulo 8 – Qualidade da Energia Elétrica”, 2010.
[16] ABINEE, “Propostas para inserção da energia solar fotovoltaica na matriz elétrica brasileira, 1ª edição, 2012.
[17] CCEE, Disponível em: http://www.ccee.org.br, acesso em 10/01/2016.