Cálculo de tensões induzidas – valores confirmados por medições (Segunda parte)

Edição 70 – Novembro de 2011
Por Sérgio Toledo Sobral

A primeira parte da medição de Kaufman mostra que quando ocorre um defeito à terra em um condutor situado no interior de um tubo de aço, aterrado em uma malha de terra local de cobre pelas duas extremidades, a quase totalidade da corrente retorna ao gerador pelo tubo de aço e não pela malha.

A segunda parte da medição de Kaufmann é semelhante à primeira, mas considera um condutor adicional de cobre interno ao tubo de aço ligado pelas duas extremidades ao mesmo tubo. A medição mostra como a corrente de retorno se subdivide entre o tubo e o condutor de cobre adicional interno.

A terceira parte deste artigo irá mostrar que é possível, utilizando apenas a Lei Circular de Ampère, calcular quase exatamente os valores de corrente e de tensão medidos numa experiência feita no Laboratório da USP em 2007. A medição utilizou uma cordoalha de cobre isolada de 50 mm² instalada no interior de um tubo de aço de 33,5 mm de diâmetro, com 9,5 mm de espessura da sua parede.

A primeira parte da experiência da USP consistiu em injetar uma corrente de 50,77 A no condutor de cobre interno e medir a diferença de potencial induzida ao longo do tubo de aço. A segunda parte consistiu em injetar uma corrente de 50,9 A no tubo de aço e calcular a diferença de potencial induzida ao longo da cordoalha de cobre interna.

Medição de Kaufmann – Parte I

O arranjo da medição de campo é exibido na Figura 1 e as distâncias utilizadas nos cálculos são mostradas na Figura 2, que caracteriza os seguintes segmentos, em metros:

ab=0,00585 ac=0,03404 ad=0,03805 ae=0,3042 af=0,3048

gh= 0,00585 gi=0,3042 gj= 0,2667. 

Figura 1 – Arranjo do teste.

 

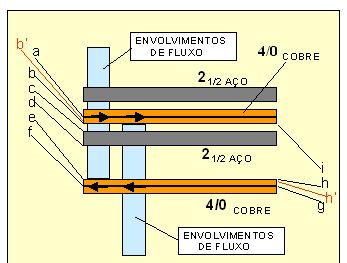
Figura 2 – Caracterização das distâncias.

Figura 3 – Circuito equivalente

Cálculo das componentes reativas de (Z₃) e (Z₁₃)

Utilizando a Lei Circuital de Ampère, como explicado em detalhe a seguir, foram calculados os seguintes valores de reatâncias indutivas, como mostrados na Figura 3:

X_AIR1=0,00940W corresponde aos envolvimentos de fluxo no ar que vão da superfície do condutor (1) até o condutor (2). Inclui também os envolvimentos de fluxo parciais no interior do cobre do condutor (1) nas proximidades de sua superfície. Não inclui os envolvimentos de fluxo no trecho (cd), no interior do tubo de aço (3).

X_AIR2=0,00966 W corresponde aos envolvimentos de fluxo no ar que vão da superfície do condutor (2) até o condutor (1). Inclui também os envolvimentos de fluxo parciais no interior do cobre do condutor (2) nas proximidades de sua superfície. Como o condutor (3) não é concêntrico com (2), ele não afeta os envolvimentos de fluxo causados pela corrente em (2).

X_INT=0,000355 W ocorre devido ao envolvimentos de fluxo causados pela corrente no condutor (1) ao atravessar o trecho (cd) do condutor de aço (3).

X_STEEL =0,0 essa parcela só é necessária quando a espessura do condutor de aço é muito grande, como no caso do teste da USP, a ser analisado na terceira parte deste artigo.

Cálculo dos componentes resistivos de (Z₃)

 

R_4/0=(0,00016 W/m).(30,48)=0,00488 W, resistência do condutor de cobre no interior do tubo de aço.

r_TUBE = (0,15(10^-6) W.m)/( p(0,03806² – 0,03404²)) =0,0001647W/m

 R_TUBE =(30,48).(0,000164)=0,00502 W, resistência longitudinal do tubo de aço

Cálculo da impedância longitudinal (Z₃) do tubo

Z₃ =(R_{4/0 +}R_TUBE)+j(X_INT+X_AIR1+X_AIR2)

Z₃ =(0,00488+0,00502)+j(0,000355 +0,00940 +0,00966)

Z₃=0,0099+j 0,01942 = 0,0218 /62,99⁰ W

Cálculo da impedância mútua (Z₁₃) entre o condutor interno e o tubo de aço

Z₁₃ =0.0 +j(X_INT+X_AIR1+X_AIR2)

Z₁₃ =0.0+j 0,01942 = j 0,01942 /90⁰ W 

Cálculo da corrente autoneutralizada (I_R) que percorre o tubo de aço aterrado nas extremidades

I= 12310 /0.0 A percorre o condutor de cobre dentro do tubo de aço

I_R= -I (Z₁₃/Z₃)= – 12310 (0,891 /27.0⁰) = 10968A

Valor medido por Kaufmann = 11090A

Cálculo da reatância (X_AIR1)

Essa reatância é devida aos envolvimentos de fluxo circulando no ar, que vão do condutor de cobre interno (1) até o condutor de cobre da malha (2) – ver Figura 1. Esses envolvimentos de fluxo correspondem aos trechos (de) e (b’c).

No trecho (de), os envolvimentos de fluxo percorrem o ar no trecho que vai da superfície externa do tubo de aço (3) até o condutor de cobre da malha de terra (2) (ver Figuras 1 e 2). Esses envolvimentos de fluxo criam uma parcela da reatância (X_AIR1).

No trecho (bc), os envolvimentos de fluxo percorrem o ar entre a superfície externa do tubo de cobre de raio (ab) e a superfície interna do tubo de aço, de raio (ac). Esses envolvimentos de fluxo criam outra parcela da reatância (X_AIR1).

Seria necessário calcular ainda a parcela de reatância criada pelo fluxo interno no cobre, que se mantém próxima da superfície do condutor de cobre (1). Esse cálculo adicional pode ser evitado com o procedimento de reduzir o raio do condutor de cobre de (ab) para (ab’) =(ab).(0,7788). Nesse caso, os envolvimentos de fluxo no trecho (b’c) incluem todos os envolvime

ntos de fluxo entre o condutor interno e a superfície interna do tubo de aço:

m_r = 1,0 para o ar e para o cobre

ab’=(0,7788).(0,00585)=0,00456

L₁ = (2.(m_r).10^-7).[ln(ac/ab’)+ ln (ae/ad)]

 = (2.(1).10^-7).[ln(0,03404/0,00456)+ln(0,3042/0,03805)]

 =8,18(10^-7) h/m

x_AIR1= 2.p.f.L₂= 0,0003083 W/m

X_AIR1= (30,48).(x_AIR1)= 0,00940W 

Cálculo da reatância (X_AIR2)

Essa reatância é devida aos envolvimentos de fluxo circulando no ar, do condutor de cobre da malha (2) até o condutor de cobre (1), interno ao tubo de aço, mostrados na Fig.1. Como o condutor de aço (3) não é concêntrico com (2), o tubo de aço praticamente não afeta o valor dos envolvimentos de fluxo em apreço.

Seria necessário calcular ainda a parcela de reatância criada pelo fluxo interno no condutor (2) de cobre, que se mantém próxima da superfície do condutor. Esse cálculo adicional pode ser evitado com o procedimento de reduzir o raio do condutor de cobre de (gh) para (gh’) =(gh).(0,7788). Nesse caso, os envolvimentos de fluxo no trecho (gh’) incluem todos os envolvimentos de fluxo relativos a (X_AIR2)

m_r = 1,0 para o ar e para o cobre

gh’ = (0.00585).(0.7788)=0,00456 m

L₂ = (2.(m_r).10^-7).ln(gi/gh’)=(2.(1).10^-7).ln(0,3042/0,00456)

= 8,40(10^-7)h/m

x_AIR2= 2.p.f.L₂= 0,000317 W/m

X_AIR2= (30,48). (x_AIR2)= 0,00966 W

Cálculo da reatância (X_INT)

A metodologia de cálculo [1] foi desenvolvida para calcular os envolvimentos de fluxo parciais que existem nas proximidades de um condutor tubular de aço, pelo qual circula corrente. Neste caso, o efeito eletromagnético equivalente das diversas camadas concêntricas de corrente que percorrem o tubo de aço é semelhante ao que haveria se ela estivesse percorrendo um condutor sólido situado no centro do tubo.

Em contrapartida, quando existe um condutor sólido conduzindo corrente no centro de um tubo de aço, são criados envolvimentos de fluxo semelhantes nas proximidades da superfície externa do condutor de aço. Os resultados das medições do Lactec, de Kaufmann e da USP mostram que o valor da permeabilidade relativa do aço a ser considerada nos cálculos para o tubo de aço é de mr= 4.4.

É provável que esse valor tão pequeno para a permeabilidade relativa do tubo de aço seja causada pela posição do mesmo em relação ao circuito magnético geral, onde os envolvimentos de fluxo percorrem grandes extensões de ar.

mr= 4.4

ad= r_{3 =} 38.055 mm=0.03806 m

ac= r_{3i =} 34.04 mm=0.03404 m

ae=0.3042 m

x_INT=2.p.60.mr.K₁.K₂, in W/m with:

K1=2.10^-7/(r₃²-r_3i²)² =2.3807

K2=(r₃⁴-r_3i⁴) /4 – (r_3i²).(r₃²-r_3i²) + r_3i⁴.ln(r₃/r_3i)=(2,95).10^-9

x_INT = 1,165(10^-5) W/m

X_INT =(30.48).(x_INT) = 0.000355 W

Cálculo da reatância (X_STEEL)

Quando o raio interno de um tubo de aço que tem um condutor em seu interior é menor (0,7788) ao seu raio externo, existirão envolvimentos de fluxo adicionais percorrendo o tubo que caracterizam a reatância (X_STEEL). Nesse caso, o cálculo dessa reatância é feita com valores de (mr) mais elevados, geralmente maiores que 100, dependendo da curva de magnetização do aço do tubo. Isso é ilustrado no caso da medição da USP, a ser tratado na terceira parte do artigo.

No presente caso tem-se:

 

(0.7788).(ad)= (0,7788).( 0,03805)=0,0296

0,0296 < ac=0,03404, em m

Logo: (X_STEEL)=0,0

Medição de Kaufmann – Parte 2

A Figura 4 mostra que, nessa parte do teste, Kaufmann instalou um condutor de cobre 4/0 interligado pelas duas extremidade a superfície interna do tubo (3). Este condutor de cobre adicional tem impedância (Z₃’) e (Z₁₃’) com valores muito próximos das impedâncias (Z₃) e (Z₁₃’) do tubo (3):

Z’₃ =(R_{4/0 +} R_4/0)+j(X_INT+X_AIR1+X_AIR2)

Z’₃ =(0.00488+0.00488)+j(0.000355 +0.00940 +0.00966)

Z’₃=0.0098+j 0.01942 = 0,0218 /62.99W

Z’₁₃ =0.0 +j(X_INT+X_AIR1+X_AIR2)

Z’₁₃ =0.0+j 0.01942 = 0.01942 /90

Figura 4 – Inclusão de um condutor de cobre interno.

Como o condutor de cobre adicional e o tubo de aço estão operando em paralelo, a corrente de retorno (I_R= 10968 A) se subdivide pelo condutor de cobre adicional e pelo condutor (3) em partes praticamente iguais. Esse fato está perfeitamente de acordo com as medições de Kaufmann.

Conclusões

O artigo mostra como calcular impedâncias próprias e mútuas em circuitos de corrente alternada, utilizando exclusivamente a Lei Circuital de Ampère, sem a necessidade de complexas operações com campos elétricos ou magnéticos. Mostra também como calcular a tensão induzida em condutores situados no interior de cabos blindados e de tubos metálicos.

Nessa segunda parte do artigo mostra-se como utilizar a Lei Circuital de Ampère quando o indutor está no interior de um tubo metálico. Os resultados calculados são quase iguais aos valores medidos.

Se os mesmos cálculos fossem feitos utilizando a Teoria de Campo, seria necessário calcular os campos elétricos e magnéticos envolvidos, utilizando cálculo vetorial e integrações feitas ao longo de trajetórias escolhidas pelo calculista. Deve ser observado que não chegou a nosso conhecimento a existência de uma metodologia utilizando Teoria de Campo que permita a execução de cálculos semelhantes.

Agradecimento

O autor gostaria de agradecer a Celso Luiz P. Mendes pela menção da medição de Kaufmann [2], que não conhecia e ilustra muito bem a importância da corrente autoneutralizada.

Referências

[1] Sobral,Sérgio Toledo (ST&SC), Peixoto,Carlos A.O, Amon, Jorge F,Tavares (FURNAS), Geraldo Martins (UFF), Izycki, Marcos José (FURNAS), Rigueira, Alexandre (UFF) “Advantages of Steinmetz Circuit Theory Over Schelkunoff Transfer Impedance Theory”. IEEE Transactions on Power Delivery, October 2009, Volume 24, Number 4, ITPDE5 (ISSN 0885-8977) pp-1876-1882

[2] Kaufmann R.H. “Some fundamentals of equipment grounding circuit design” AIEE Trans. Appl.& Industry NOV1954 pp 227-232.

*Sérgio Toledo Sobral é engenheiro eletricista. Foi superintendente do Departamento de Estudos de Sistemas, diretor de projetos da Internacional de Engenharia S.A. e consultor especial no Projeto Itaipu. Desde 1990, está com sua própria companhia, a ST&SC Serviços Técnicos Ltda.